Предприятие выпускает 2 вида продукции А и В, для производства которых используется сырье трех видов. На изготовление единицы изделия (Решение → 14169)

Заказ №38664

Предприятие выпускает 2 вида продукции А и В, для производства которых используется сырье трех видов. На изготовление единицы изделия А требуется затратить сырья каждого вида 13, 4 и 3 кг соответственно, а для единицы изделия В – 2, 4 и 14 кг. Производство обеспечено сырьем каждого вида в количестве 260, 124 и 280 кг соответственно. Стоимость единицы изделия А составляет 12 руб., а единицы изделия В – 10 руб. Требуется составить план производства изделий А и В, обеспечивающий максимальную стоимость продукции. Решить задачу: А) геометрически; Б) симплекс-методом.

Решение:

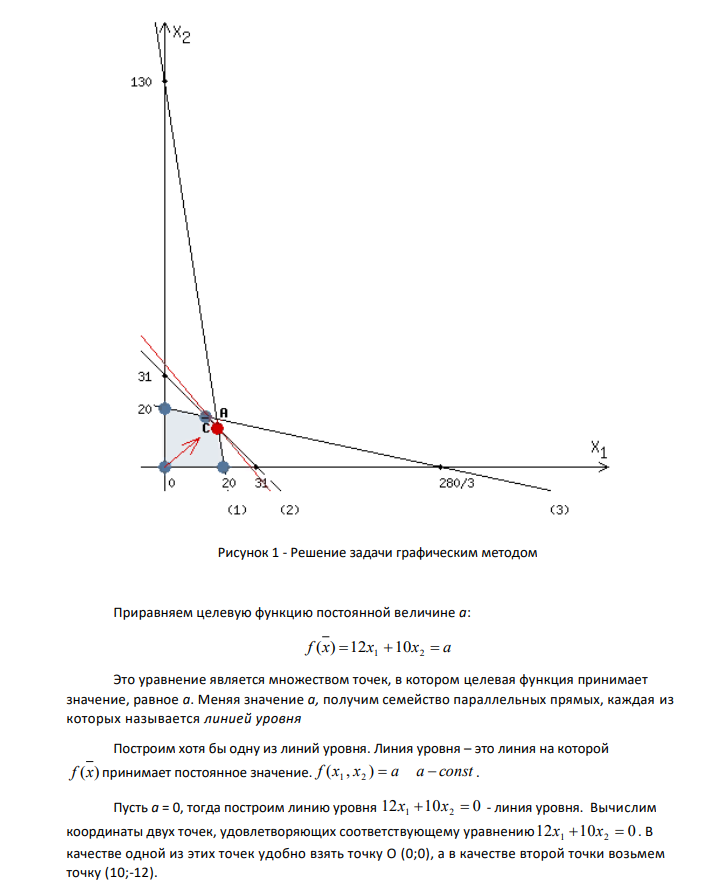
66 1. Сформулируем экономико-математическую модель задачи Вводим переменные. Пусть х1 – количество изделий вида А, х2 – количество изделий вида В. Составляем функцию цели. Необходимо максимизировать прибыль. 1 2 1 max f (x) c x 12х 10х n j   j j    Экономический смысл: 1 2 12х 10х - общая прибыль от производства изделий обоих видов. Составляем ограничения. Функциональные ограничения (по видам сырья):            3 14 280 4 4 124 13 2 260 1 2 1 2 1 2 х х x х x x Прямое ограничение. Т.к. количество изделий не может быть отрицательным числом, то , 0 x1 x2  . Таким образом, имеем задачу линейного программирования: Найти вектор ( , ) 1 2 x  x x , при котором функция цели 12 1 10 2 f (x)  x  x достигает максимального значения, при ограничениях:               , 0 3 14 280 4 4 124 13 2 260 1 2 1 2 1 2 1 2 x x х х x х x x 2. Найдем оптимальный план графическим методом (геометрически) а) Построим область допустимых решений Решением каждого ограничения системы является полуплоскость с граничащей ей прямой. 13х1  2х2  260 (1) Построим прямую 13х1  2х2  260 . Она проходит через точки (0;130) и (20;0). Для того чтобы определить, какая плоскость удовлетворяет неравенству, необходимо выбрать любую точку не принадлежащую прямой. Выберем точку начала координат (0;0), подставим в неравенство 13 2 260 х1  х2  и получим 0 < 260. Данное утверждение является верным, следовательно, неравенству соответствует нижняя полуплоскость, включающая точку (0;0). 67 4 4 124 х1  х2  (2) Построим прямую 4 4 124 х1  х2  . Она проходит через точки (0;31) и (31;0). Выберем точку начала координат (0;0), подставим в неравенство 4 4 124 х1  х2  и получим 0 < 124. Данное утверждение является верным, следовательно, неравенству соответствует нижняя полуплоскость, включающая точку (0;0). 3х1 14х2  280 (3) Построим прямую 3х1 14х2  280 . Она проходит через точки (0;20) и (280/3;0). Выберем точку начала координат (0;0), подставим в неравенство 3х1 14х2  280 и получим 0 < 280. Данное утверждение является верным, следовательно, неравенству соответствует нижняя полуплоскость, включающая точку (0;0). 0 x1  0 x1  - решение – прямая, совпадающая с осью ОХ2 0 x1  - решение – правая полуплоскость. 0 x2  0 x2  - решение – прямая, совпадающая с осью ОХ1 0 x2  - решение – верхняя полуплоскость. Т.е. ограничения х1  0 и х2  0 показывают, что решение системы находится в I четверти системы координат. Пересечение этих полуплоскостей, каждая из которых определяется соответствующим неравенством системы и удовлетворяет условиям, определяет выпуклый многоугольник. Данный многоугольник – область допустимых значений. Любая точка этой области является допустимым решением задачи. б) Найдем оптимальное решение Оптимальное решение может быть только в угловых точках многоугольника. Чтобы найти оптимальное решение можно найти координаты всех угловых точек многоугольника, вычислить значение целевой функции во всех угловых точках. Наибольшее из этих значений и будет максимальным значением целевой функции, а координаты соответствующей угловой точки – оптимальным решением. Существует другой способ, который позволяет графически сразу найти угловую точку, соответствующую оптимальному решению. Для этого построим линию уровня. 68 Рисунок 1 - Решение задачи графическим методом Приравняем целевую функцию постоянной величине а: f (x) 12х1 10х2  а Это уравнение является множеством точек, в котором целевая функция принимает значение, равное а. Меняя значение а, получим семейство параллельных прямых, каждая из которых называется линией уровня Построим хотя бы одну из линий уровня. Линия уровня – это линия на которой f (x) принимает постоянное значение. f (x , x )  a a  const 1 2 . Пусть а = 0, тогда построим линию уровня 12x1 10x2  0 - линия уровня. Вычислим координаты двух точек, удовлетворяющих соответствующему уравнению 12x1 10x2  0 . В качестве одной из этих точек удобно взять точку О (0;0), а в качестве второй точки возьмем точку (10;-12). Для определения направления движения к оптимуму построим вектор-градиент С  , координаты которого являются частными производными функции f(x), т.е. С  =(12;10). 69 Чтобы построить этот вектор, нужно начало координат соединить с точкой (12; 10). Поскольку задача стоит на максимизацию, перемещаем линию уровня по направлению вектораградиента С  . Максимума ( , ) 1 2 f x x достигает в угловой точке А. Находим координаты т. А. Она находится на пересечении прямых, образуемых ограничениями (1) и (2):        4 4 124 13 2 260 1 2 1 2 x x x x Получаем:      13 18 2 1 x x Находим значение функции цели: max f (x)  12×18+10×13 = 346 Ответ: max f (x)  346 при х1 = 18, х2 = 13. Экономический смысл: Максимальная прибыль от реализации изделий обоих видов составит 346 руб. если производить 18 единиц изделий вида А и 13единиц изделий вида В. При этом сырье. Соответствующее ограничениям (1) и (2) (т.е. сырье первого и второго видов) используется в оптимальном плане полностью. Данные виды сырья являются дефицитными, ограниченные запасы сырья 1-го и 2-го видов сдерживает рост производства продукции общей прибыли. 3. Решим задачу симплексным методом Проведем задачу к каноническому виду Канонический вид записи модели, т.е. когда система функциональных ограничений состоит только из уравнений с неотрицательной правой частью. В левые части неравенств вводим неотрицательные добавочные переменные со знаком «+» (т.к. знак неравенства ≤ ):                  , , , , 0 3 14 280 4 4 124 13 2 260 1 2 3 4 5 1 2 5 1 2 4 1 2 3 x x x x x х х х x х х x x х Находим первое допустимое базисное решение 1-ое решение проще найти, если среди n переменных есть m таких, коэффициенты при которых образуют единичную матрицу порядка m. Тогда эти переменные можно взять за основные. Остальные (n-m) будут не основные. 70 Координаты переменных 3 4 5 x , x , х образуют единичную матрицу 3-го порядка. Их берем за основные. Основные переменные - 3 4 5 x , x , х Неосновные переменные - 1 2 x , x n – количество переменных (n = 5); m – количество основных переменных (m = 3); Находим исходное допустимое опорное (базисное) решение. Базисное решение – решение, при котором неосновные переменные равны нулю x1  0, x2  0 , тогда подставляя значения переменных в уравнения системы ограничений получаем.             280 124 260 , 0 5 4 3 1 2 1 x x x x x x - 1-ое опорное решение. Решение является допустимым, т.к. нет отрицательных значений. Находим значение целевой функции: f (x1 )  12×0+10×0 = 0 Дальнейшее решение оформляем в симплексные таблицы. i c - коэффициенты при основных переменных в функции цели f (x) ; j c - коэффициенты при переменных функции цели. Таблица 5